Many-Body Physics Explored in a Spin-1 Bose-Einstein Condensate
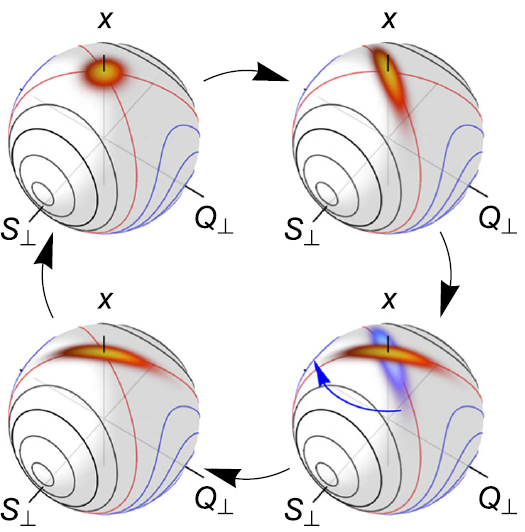
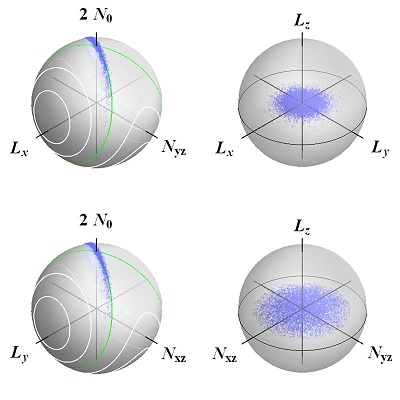
We generate spin squeezed ground states in an atomic spin-1 Bose-Einstein condensate tuned near the quantum critical point between the polar and ferromagnetic quantum phases of the interacting spin ensemble. In contrast to typical non-equilibrium methods for preparing atomic squeezed states by quenching through a quantum phase transition, squeezed ground states are time-stationary and remain squeezed for the lifetime of the condensate. A squeezed ground state with a metrological improvement up to 6-8 dB and a constant squeezing angle maintained over 2 s is demonstrated.
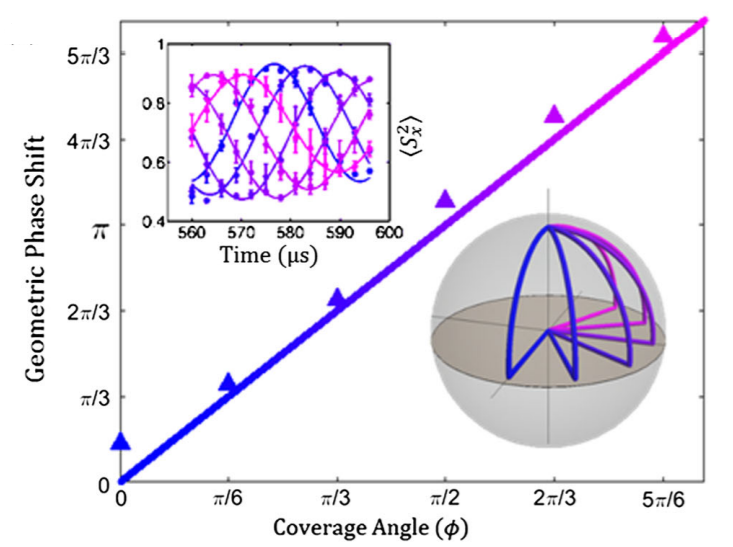
The spin vector of a spin-1 system, unlike that of a spin-1=2 system, can lie anywhere on or inside the Bloch sphere representing the phase space. As a consequence, the geometrical and topological properties of the spin-1 phase space of quantum states are richer and require a generalization of Berry’s phase. For special trajectories passing through the center of the Bloch sphere (singular loops), the geometric phase has a non-Abelian nature. Here, we experimentally explore this geometric phase for singular loops in a spin-1 quantum system using ultracold 87Rb atoms confined in an optical trap using microwave and rf control fields.
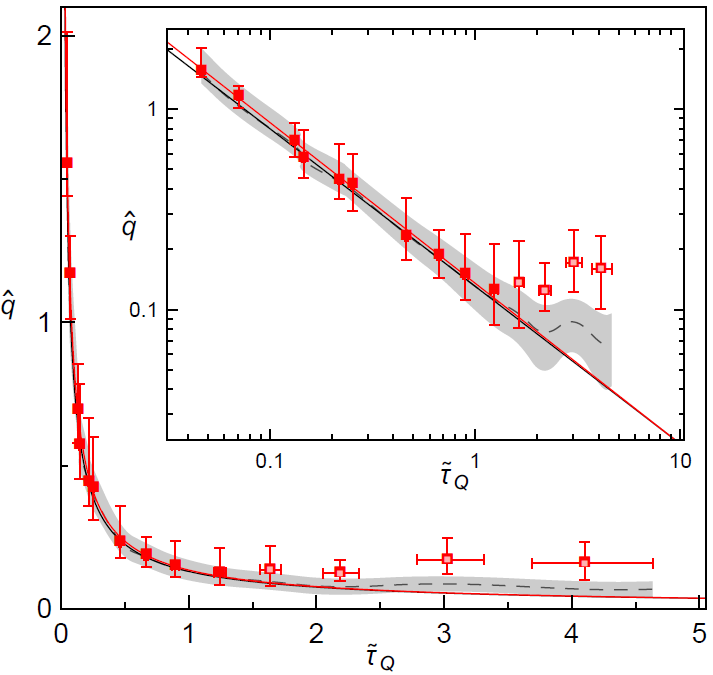
The Kibble-Zurek mechanism (KZM) primarily characterizes scaling in the formation of topological defects when a system crosses a continuous phase transition. The KZM was first used to study the evolution of the early universe, describing the topology of cosmic domains and strings as the symmetry-breaking phase transitions acted on the vacuum fields during the initial cooling.
A ferromagnetic spin-1 87Rb Bose-Einstein condensate (BEC) exhibits a second-order gapless quantum phase transition due to a competition between the magnetic and collisional spin interaction energies. Unlike the situation in extended systems where the KZM is illustrated by topological defects, we focus our study on the temporal evolution of the spin populations and observe how the scaling of the spin dynamics depend on how fast the system is driven through the critical point. In our case, the excitations are manifest in the temporal evolution of the spin populations illustrating a Kibble-Zurek type scaling, where the dynamics of slow quenches through the critical point are predicted to exhibit universal scaling as a function of quench speed.
The KZM has been studied theoretically and experimentally in a large variety of systems. There has also been a tremendous interest in the KZM in the cold atoms community in recent years. It has been observed not only in ion chains and in atomic gases in optical lattices, but also in Bose gases through the formation of vortices or solitons. The KZM in the context of crossing the quantum phase transition in a ferromagnetic BEC has been theoretically studied, but this study is the first experimental investigation of this phenomenon.
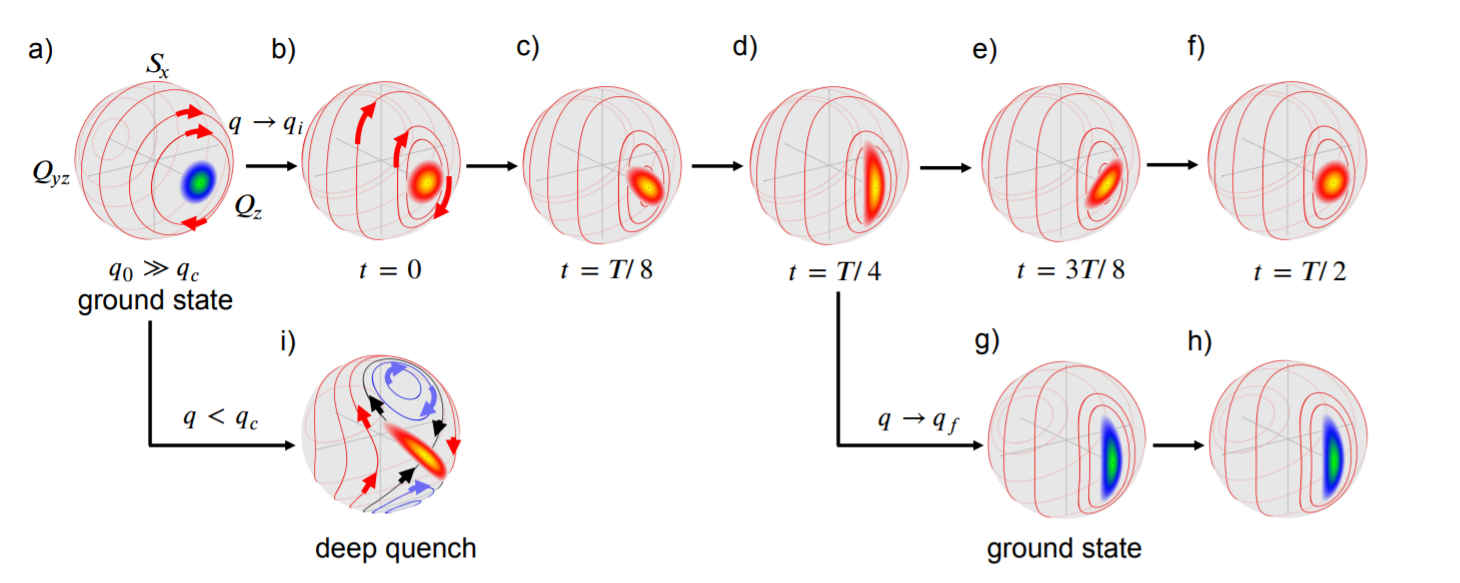
Many classical systems, such as the Kapitza's pendulum, can be dynamically stabilized by vibrating a pivot point. Dynamic stabilization has a broad range of applications including rf ion traps, mass spectrometers, and particle synchrotrons. Recent advancements in ultracold atomic physics have enabled us to investigate an unstable equilibrium phenomenon of an interacting spin-1 Bose-Einstein condensate.
We employ a spin-1 Bose condensate satisfying the single mode approximation initialized to an unstable (hyperbolic) fixed point of the phase space. The unstable fixed point is located at the intersection of two phase-separated manifolds - phase-winding and oscillatory phase orbits, whose dynamics are well described by a classical non-rigid pendulum. To initiate spin dynamics, the condensate is rapidly quenched below the quantum critical point by lowering the magnetic field to 220mG generating Gaussian squeeze states at early times and a rich variety of non-Gaussian states at later times that eventually destabilize the system. In order to dynamically stabilize the system we periodically pulse the condensate with microwave pulses. These pulses are engineered to systematically control the phase of the condensate through periodic rotations of the manifolds that are delineated by the separatrix.
Provide a theoretical background to understand generation and measurement of squeezed states produced by spin mixing in a spinor Bose-Einstein Condensate (BEC). Calculate the amount of squeezing as well as its time evolution for comparison to experimental results. Simulate quantum control techniques used to manipulate the squeezing quadrature for measurement and eventually state preparation of spin squeezed states for quantum simulation and metrology.
We have created a Bose-Einstein condensate (BEC) of 87Rb atoms directly in an optical trap. We employ a quasielectrostatic dipole force trap formed by two crossed CO2 laser beams. Loading directly from a sub-Doppler laser-cooled cloud of atoms results in initial phase space densities of ~1/200. Evaporatively cooling through the BEC transition is achieved by lowering the power in the trapping beams over ~2 s. The resulting condensates are F = 1 spinors with 3.5x104 atoms distributed between the mF = (-1,0,1) states.
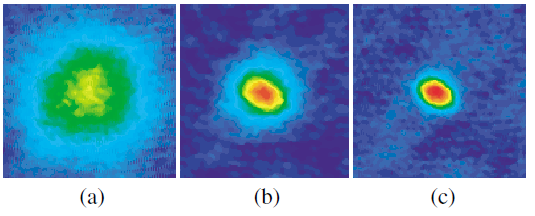
Absorptive images (false color) of atomic cloud after 10 ms free expansion for different final trap laser powers. (a) Thermal cloud above BEC transition (P=280 mW), (b) thermal condensate mixture (P=260 mW), and (c) pure condensate (P=190 mW). Field of view is 350 um.
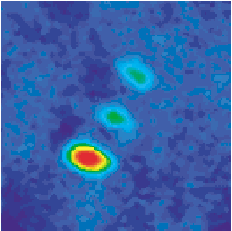
Absorptive image of atomic cloud after 10 ms free expansion in a Stern-Gerlach magnetic field gradient. Three distinct components are observed corresponding to F=1, mF=-1, 0, 1 spin projections from bottom to top respectively.
